萌战的博弈数学

(image credit: teralimit)

不出各位所料，2011年最萌大赛的桂冠，将在本周六于魔法少女小圆的两大人气角色中决出。这个结果并不让我们惊讶，以小圆BD评论音轨的声优告白情况看，掉头王后麻美学姐与吃货枪兵红毛杏子的确是人气最高的两位角色，可以走到决赛会师可谓实至名归。

说实话店长对萌战的最终获胜者没有看法，红毛也好，学姐也罢，恭喜赢家，安慰输家，大家尽兴，结果随它——这种最终投票量常常比BD销量还低的比赛，其实际参考性可想而知。讽刺的是，我对这投票背后的数字博弈却兴趣盎然，于是就有了这篇醉翁之意不在酒的文章。

其实我们今天要谈的话题还是蛮入流的，“红毛vs学姐，你更支持两人中的哪位角色？”

分布01

• 学姐 (52%, 65 Votes)
• 红毛 (48%, 59 Votes)

Total Voters: 124

 Loading ...

红毛党与学姐党，下注完成了吗？现在请放下你心头纠结的情绪，考虑这个新条件，“假设你的目的不是支持谁，而是纯粹猜谁会胜出，而且猜对的人客栈均会赠送1,000大元手办购物礼券，请问现在你会猜谁获胜？”

分布02

• 红毛 (35%, 41 Votes)
• 学姐 (65%, 75 Votes)

Total Voters: 116

 Loading ...

然后是最后一个提问，“假设上面的两种投票分布是对萌战最终结果的评测，请问你认为哪个更可能是正确的？”

Which one?

• 分布01 (48%, 53 Votes)
• 分布02 (52%, 58 Votes)

Total Voters: 111

 Loading ...

投票已于2011.11.05 GMT+8 17:30结束（2011年萌战还剩5个半小时）

学过宏观经济的人应该能想起一个叫“凯恩斯选美理论”（Keynesian beauty contest）的实验，没错，就是那个凯恩斯主义的凯恩斯。它描述的是一个简单的情景——假设要你猜一场选美大赛的民众投票结果，并且猜中就有大奖，你会怎么猜？正确的做法，或者说“理智”的做法，是去猜测别人最有可能喜欢什么选手，而非选择自己最喜欢的选手。

有趣的是，这种思考可以“高阶”重复下去。我可以假设别人都是“理智”的，然后基于这种假设去选择；而别人也可以假设我假设他是理智的；然后我还能假设他假设我假设他是理智的……如此类推。凯恩斯用这个理论来解释股价变动；假设投资者都是理智的，那必定出现某些“最大笨蛋”（Greater fool theory）把它人的“理智”设想得太好，最终自己成为了那个⑨。

这就是“聪明反被聪明误”的经典案例——每个人都以为自己在思考（增加自己的价值），其实没有一个人在思考真正的问题（股票的真实价值），而是在猜别人怎么看待同样的事物（寻找最大的笨蛋）。

话题回到萌战上，半决赛小圆vs学姐的过程中就发生了同样的事情。小圆的爱好者们想利用如上策略击败学姐爱好者，他们假设学姐的投票者是“理智”的（会持续投票，到最后关头的冲击力有限），并设计在最后5分钟内刷票击溃学姐党。结果呢？他们遇到了市场的阻碍，被大量废票占用了宝贵的反超时间，最终以败北收场。从这点上看，小圆党不得不说是败在了“⑨的小聪明”上；换句话说，假设“所有阿宅都是理智”的模型过于简单；事实上“参加萌战”本身可能就是不理智的表现……

那怎么解决这种“理智”与“不理智”导致的数据浮动？延长时间。正如热爱“基础分析”（Fundamental analysis）的投资人所深信的“股价在长时间中必然反映公司自身的价值”的基本定则，萌战若把投票时间增长至1周甚至更长，它就能避免这种最后5分钟的大战；虽然同时也会给另一些团体留下更多刷票的机会。

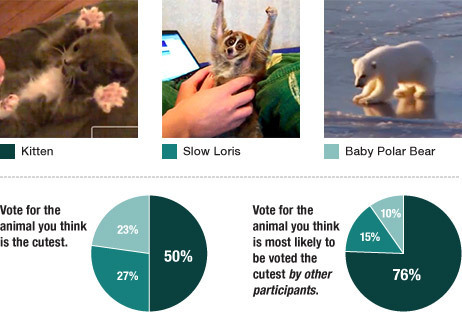
正所谓殊途同归，只要取样没有什么问题，时间能让本文上述的两种模式的结果趋近（但第二种模式更能看出某个事物的心态优势）。美国的全国公共广播电台（NPR，不是NTR，谢谢）曾经做过一个实验，随机选择两批观众，让他们从小猫，小懒猴，小北极熊的视频中选择他们认为最萌或他们认为别人觉得最萌的视频。结果如下——

可见当一个事物占有领先优势时（这里是小猫），它在“理智”预测中的结果会变得更为庞大，甚至如股市般虚高。

至于客栈的投票是否真的能预言最萌决赛的结果，还得看我们的旅客群都是些什么人。我觉得这里更大的问题是取样空间与偏差……不过这和博弈没啥关系了，这属于纯粹统计学的范畴。

PS: 说起统计学，各位不妨尝试回答这个经典的提问——

PPS: 最后再送大家一个Slashdot的经典投票——猜猜有多少人会和你选择一样的选项？

PPPS: 我什么都不知道……